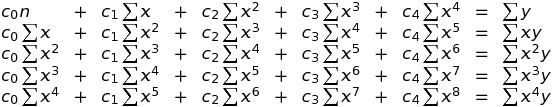
n 個の標本点を通る n-1 次式を計算するため、 必要な整式の n 個の係数を連立方程式を立てて計算する。
プログラム例 , 実行結果例 , 実行ファイル例: /class/mce/NumAnalysis/xmp08b
補間多項式について、標本点において誤差が零になることを確認せよ。
また、補間される多項式の次数が補間多項式の次数より小さい場合には、
補間される多項式の正確な係数が求まることを確認せよ。
分数関数や超越関数、あるいは
補間される多項式が補間多項式より高次の場合には、
どのような誤差が現れるか確認せよ。
この実行結果例では、二つのプログラムを同時に実行することになるため、 まず最初にそれらを互いに区別できるようにするために実行プログラムの名前を変える必要がある。
このためには、例えばコンパイル時に以下のように指定する。
cc -o executable source.c
ここでオプション -o に与えるパラメータはコンパイルして作る実行可能プログラムの名前で、
このオプションを省略した場合には a.out が使用される。
あるいは既に作成済みの実行可能プログラムに新しい名前を与えることもできて、
以下のように実行する。
mv a.out newexecutable
この例では既存の実行可能プログラム a.out の名前を newexecutable に変更している。
一次独立な関数群として、 たとえば 単項関数の列 { 1, x, x2, x3, x4 } を 選ぶとすると、連立一次方程式
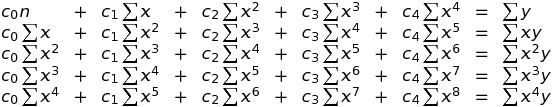
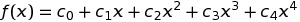は、この式のグラフと与えられた点列との垂直距離の自乗和が最小になる『良い近似式』となり、
この近似手法を最小自乗法と呼ぶ。
ここでは与えられた点列 (x, y) の値から上記の連立一次方程式の各係数を決定し、 前項で作成したプログラムに与えるべきデータを作成するためのプログラムを作成する。
プログラム例 , 実行結果例 , 実行ファイル例: /class/mce/NumAnalysis/xmp08a
近似式においては、標本点において誤差が必ずしも零とならないことを確認せよ。
分数関数や超越関数、あるいは
近似される多項式が近似多項式より高次の場合には、
どのような誤差の現れ方をするか確認せよ。
前項で開発した連立多元一次方程式の数値解を求めるプログラムに対して、
その入力データを作成するプログラムを実装して、
たとえば以下のように UNIX の pipe を用いて計算を行なう。
./xmp08a -n4 | ./xmp07a
ただし、オプション -n に与えるパラメータは、
何次の多項式で関数を近似しようとするのかを示し、
最大次数に 1 を加えたものを指定する。
この数が、求める多項式中で決定しなければいけない係数の総数となる。
コマンド行内の "|" 文字は、
左側のコマンドの標準出力をそのまま右側のコマンドの標準入力に与えることを意味し、
次のようなコマンド群と同じ効果になる。
./xmp08a -n4 > somefile
./xmp07a < somefile
ただし、 pipe を用いる場合は二つのコマンドは同時に並行して処理され、 中間ファイルも実際には使用されないことに注意せよ。