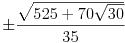 ,
x2 = x3 =
,
x2 = x3 = 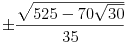
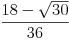 ,
W2 = W2 =
,
W2 = W2 = 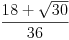
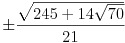 ,
x2 = x4 =
,
x2 = x4 = 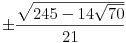 ,
x3 = 0
,
x3 = 0
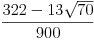 ,
W2 = W4 =
,
W2 = W4 = 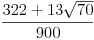 ,
W3 = 128/225
,
W3 = 128/225
積分区間を [0, 1] に規格化した公式の係数を示す。 ニュートン・コーツ公式では分点は必ずすべて等間隔である。
その分点は積分区間の両端を含むが、このことを閉じた公式であるという。
なお、ニュートン・コーツ公式には開いた公式もあるが、
これらは精度的な問題から使用される機会は少ない。
| 次数 | 重み |
|---|---|
| 1 | B0 = B1 = 1/2 |
| 2 | B0 = B2 = 1/6, B1 = 2/3 |
| 3 | B0 = B3 = 1/8, B1 = B2 = 3/8 |
| 4 | B0 = B4 = 7/90, B1 = B3 = 32/90, B2 = 12/90 |
| 5 | B0 = B5 = 19/288, B1 = B4 = 75/288, B2 = B3 = 50/288 |
| 6 | B0 = B6 = 41/840, B1 = B5 = 216/840, B2 = B4 = 27/840, B3 = 272/840 |
| 7 | B0 = B7 = 751/17280, B1 = B6 = 3577/17280, B2 = B5 = 1323/17280, B3 = B4 = 2989/17280 |
積分区間を [-1, 1] に規格化した公式の係数を示す。
また、ガウス公式では分点は両端を含まず、このことを開いた公式であるという。
ここには n<=5 の場合のみを示すが、
必要であれば n はもっと大きなものを使うこともできる。
| 分点数 | 分点 | 重み |
|---|---|---|
| 1 | x1 = 0 | W1 = 2 |
| 2 | x1, x2 = ± sqrt(3)/3 | W1 = W2 = 1 |
| 3 | x1, x3 = ± sqrt(15)/5, x2 = 0 | W1 = W3 = 5/9, W2 = 8/9 |
| 4 | x1, x4 = 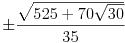 ,
x2 = x3 = ,
x2 = x3 = 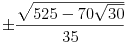
| W1 = W4 = 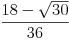 ,
W2 = W2 = ,
W2 = W2 = 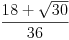
|
| 5 | x1, x5 = 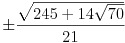 ,
x2 = x4 = ,
x2 = x4 = 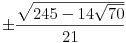 ,
x3 = 0 ,
x3 = 0
| W1 = W5 = 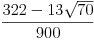 ,
W2 = W4 = ,
W2 = W4 = 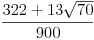 ,
W3 = 128/225 ,
W3 = 128/225
|
積分区間を [-1, 1] に規格化した公式の係数を示す。
また、チェビシェフ公式では重みはすべて一定で 2/n である。
ここには n<=5 の場合のみを示すが、
チェビシェフ公式には n=8 や n>9 の公式は存在しない。
| 分点数 | 分点 | 重み |
|---|---|---|
| 1 | x1 = 0 | Wi = 2 |
| 2 | x1, x2 = ± 1 / sqrt(3) | Wi = 1 |
| 3 | x1, x3 = ± 1 / sqrt(2), x2 = 0 | Wi = 2/3 |
| 4 | x1, x4 = 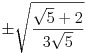 ,
x2 = x3 = ,
x2 = x3 = 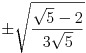
| Wi = 1/2 |
| 5 | x1, x5 = 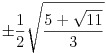 ,
x2 = x4 = ,
x2 = x4 = 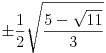 ,
x3 = 0 ,
x3 = 0
| Wi = 2/5 |