小テスト(2)

正の整数 n を与えて, xy 平面上で (-n)≦x≦n, (-n)≦y≦n となるような 整数x, y の格子点を考える.

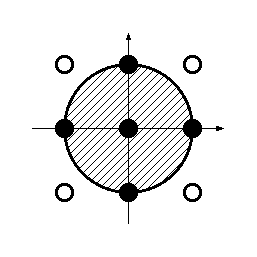
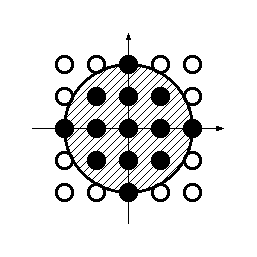
このような格子点は (2n+1)×(2n+1) 個あるわけだが, これらのうちで, 原点を中心とする半径 n の円の(円周も含めた)内側に あるものの個数を調べたい.

プログラムの入力は正の整数 n で, 出力には, まず n, 次の行に条件を満たす格子点の個数をしるす.

たとえば n = 1 とすると, 入力は 

1
となり, 出力は格子点5個 (-1,0),(0,-1),(0,0),(0,1),(1,0) が条件を満たすから 
1
5
となる.

(豆知識)これを用いると, 円の面積の公式からπの値の近似値を知ることができる. つまり
π≒(条件を満たす格子点の個数)/(n*n)