第7回課題2の解答(例)

(tex 版 psfile)
diffeq.c において、指定された値(表1)を入れて計算した結果を一つのグラフに重ねて描くと図1のようになる。この図から計算時間間隔 dt と計算精度の関係について次の事が分かる。

dt が 0.01の場合は、解析的計算結果との誤差が目立つ。
dt が 1e-3 から 1e-7 は、グラフ上はほとんど重なっていおり、解析的計算結果との誤差が非常に小さい事がわかる。
dt が 1e-8 では、再び誤差が増えており不自然な結果が得られている。
dt が 1e-9 では、初期値から全く変化しない明らかに誤った結果になっている。

計算時間間隔 0.01 秒では誤差が若干大きく、 1e-3 秒から1e-7 秒は、解析結果との誤差がほとんど見られない。このことから、計算に要する時間も考慮すると、これらの値の中では、 1e-3 秒が計算時間間隔が最適と考えられる。
この微分方程式をオイラー法で解く場合には演習での時定数 1秒の場合の結果とあせて考えると、時定数の 100 分の1 程度の時間間隔が適当と考えられる。
(補足:ここで示した最適な計算時間間隔の値は絶対的なものでは無く、一般には結果の利用目的によって異なる。)
表1 : 計算条件

入力項目	単位	Value
時定数	秒	0.1
電圧源	V	0
初期値	V	10
計算時間	秒	0.1
計算時間間隔	秒	0.01	1e-3	1e-6	1e-7	1e-8	1e-9
表示時間間隔	秒	0.01

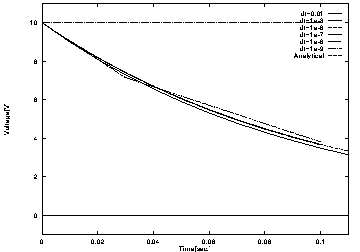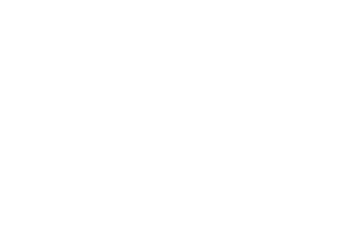
図1 : 各解法による計算結果の比較(epsfile)